Points of Continuity Belong to the Lebesgue Set

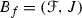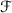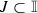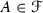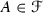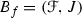In the next part of the paper, we will need the notion of an entropy of a function at a point, considered in [4, 9]. For a function f a pair is called an f -bundle if is a family of pairwise disjoint non-singleton continua in \(\mathbb {I}\) and is a connected set such that \(J\subset f(A)\) for any . If we additionally assume that \(A \subset J\) for all then will be called an f -bundle with dominating fibre.

Similarly, as in the case of an entropy of a function we define a separated set connected with an f-bundle. Let \(\varepsilon >0\), \(n\in \mathbb {N}\), 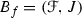be an f-bundle and 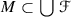. We shall say that M is \((B_f,n,\varepsilon )\) -separated if for each \(x,y\in M\), \(x\not =y\), there is such that \(f^i(x), f^i(y)\in J\) and \(|f^i(x)-f^i(y) |>\varepsilon \). Put 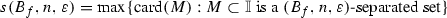. The number

$$\begin{aligned} h(B_f)=\lim \limits _{\varepsilon \rightarrow 0} \limsup \limits _{n \rightarrow \infty } \frac{1}{n}\log s(B_f,n,\varepsilon ) \end{aligned}$$

is called an entropy of an f -bundle \(B_f\). It is worth adding that if 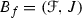is an f-bundle with dominating fibre and 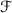is finite then 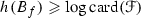[9].

We shall say that a sequence of f -bundles 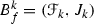converges to a point \(x_0\) (in short \(B^n_f \xrightarrow [\scriptscriptstyle n\rightarrow \infty \,]{} x_0\)), if for any \(\varepsilon >0\) there exists \(k_0\in \mathbb {N}\) such that 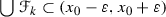and \((f(x_0)-\varepsilon ,f(x_0)+\varepsilon )\cap J_k\not =\varnothing \) for any \(k\geqslant k_0\). An entropy of a function f at \(x_0\in \mathbb {I}\) [4] is the number

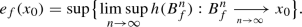
Let 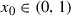and 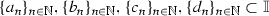be sequences such that 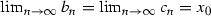and \(c_{n}<d_n<c_{n+1}\) and \(b_{n+1}<a_n<b_n\) for any \(n\in \mathbb {N}\). An interval set at a point \(x_0\) is the set given by the following formula:

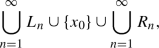
where 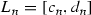and 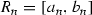for \(n\in \mathbb {N}\). Similarly, we define a right-(left-)hand interval set at a point 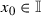. To shorten the notation, f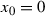or or 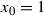an interval set at a point \(x_0\) we will be a right-hand or a left-hand interval set at this point, respectively. Let 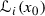denote the set of all interval sets at a point \(x_0\).

For any 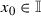and 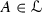if there exists the limit

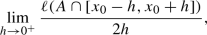
then we call it the density of a set A at a point \(x_0\). Similarly, we define the right-(left-)hand density of a set at a point. If 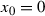or 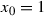then we consider suitable one-sided density of this set at \(x_0\). If the density of A at a point \(x_0\) is equal to 1, then we say that \(x_0\) is a density point of a set A.

We shall say that f is strongly 0-approximately continuous at 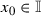if there exists a set 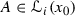such that \(x_0\) is a density point of A, \(\lim _{A\ni x\rightarrow x_0} f(x)=f(x_0)\) and \(h(f,A)=0\).

It is easy to present an example of a function which is strongly 0-approximately continuous at any point from \(\mathbb {I}\) (the constant function has this property). Simultaneously, the function from [5, Theorem 2.4] is an example of a function which is not strongly 0-approximately continuous at any point from \(\mathbb {I}\). One can ask, whether there exists a continuous function with such a property.

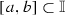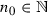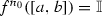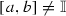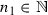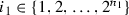Let \(f:\mathbb {I}\rightarrow \mathbb {I}\) be the tent map. Obviously, \(h(f)=\log 2\) (see [10, p. 94]). Moreover, for any non-degenerate interval one can find the number for which . Indeed, without loss of generality we may assume that . Then there exist and such that

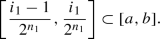
From the definition of the tent map it follows that 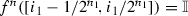for any \(n> n_1\). Let \(n_0=n_1+1\). Since 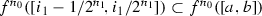, we obtain 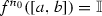. From Lemma 1.2 it follows that 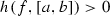for any interval 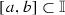. Hence, we immediately obtain that f is not strongly 0-approximately continuous at any point from \(\mathbb {I}\). Indeed, assume that f is strongly 0-approximately continuous at \(x_0\). Then there exists an interval set 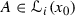such that \(h(f, A)=0\). On the other hand, there exists a closed non-degenerate interval 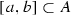for which 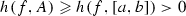, which is a contradiction.

In the paper [5] there were considered functions 0-approximately continuous at a point. We shall say that f is 0-approximately continuous at 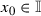if there exists a set 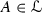such that \(x_0\) is a density point of A, \(\lim _{A\ni x\rightarrow x_0} f(x)=f(x_0)\) and \(h(f,A)=0\). Obviously, if a function f is strongly 0-approximately continuous at a point \(x_0\), then it is 0-approximately continuous at this point. The inverse implication does not hold. Indeed, the characteristic function of the set 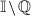is 0-approximately continuous at any point from 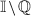and it is not strongly 0-approximately continuous at this point.

In the paper [8] there was introduced the notion of an odd point for dynamical systems. For a function \(f:\mathbb {I}\rightarrow \mathbb {I}\) this definition is as follows. We shall say that 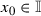is an odd point of a function f if \(x_0\) is an almost stable point of f (i.e. 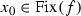and for any \(\varepsilon >0\) there are \(\delta >0\) and \(i_0\in \mathbb {N}\) such that for each \(i\geqslant i_0 \) and \(x\in \mathbb {I}\) if \(|x-x_0|<\delta \) then \(| f^i(x)-x_0|<\varepsilon \)) and an entropy of f at the point \(x_0\) is infinite. Evidently, if f is a continuous function and \(x_0\) is an odd point of f, then \(x_0\) is a stable point of f. It means 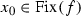and for any \(\varepsilon >0\) there is \(\delta >0\) such that for each \(i\in \mathbb {N}\) and \(x\in \mathbb {I}\) if \(|x-x_0|<\delta \) then \(| f^i(x)-x_0|<\varepsilon \) (see [8]).

In another paper [5] there were considered functions attracting positive entropy at a point. Let \(f\in \mathfrak {D}\) and 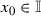. We say that f attracts positive entropy at a point \(x_0\) if for any \(\varepsilon >0\) there exists \(\delta >0\) such that for each function \(g\in B_{\rho _u}(f, \delta )\cap \mathfrak {D}\) we have \(h(g,(x_0-\varepsilon , x_0+\varepsilon )\cap \mathbb {I})>0\), where \(B_{\rho _u}(f, \delta )\) is the open ball with center at f and radius \(\delta \) with respect to the metric of uniform convergence.

Definition 2.1

Let \(f:\mathbb {I}\rightarrow \mathbb {I}\) be a Darboux function. We say that \(x_0\) is a peculiar point of the first kind of f if

1. (A1)

   \(x_0\) is an odd point of f;

2. (B1)

   f is 0-approximately continuous at \(x_0\) and it is not strongly 0-approximately continuous at \(x_0\);

3. (C1)

   f attracts positive entropy at \(x_0\).

If in this definition condition (B1) is replaced by the condition

\((\mathrm{B}1^{\prime })\) :

f is strongly 0-approximately continuous at \(x_0\),

then we obtain the definition of a peculiar point of the second kind.

The notion of a peculiar point seems to be very complex. As the name of such a point indicates, it describes a very special situation, when around a point a function is stable on a big set (in the sense of Lebesgue measure) and, simultaneously, it is not only strongly chaotic, but there takes place the so-called entropy black hole phenomenon as well: if another function is close to a function possessing a peculiar point, then its entropy is positive in any neighbourhood of this point (many mathematicians identify this with the chaotic behaviour of a function). So it is natural to ask, if having a peculiar point is a random, incidental property of a function or it is frequent (in some sense). The same question can be posted for continuous functions.

As it was mentioned earlier, in the real analysis theory, almost continuous functions play a very important role. This notion was introduced in 1959 by Stallings in [11]. The main theorem of this work shows that any \(\Gamma \)-neighbourhood of an almost continuous function contains a continuous function with a peculiar point (of the first or second kind).

Recall the definition of an almost continuous function: we say that a function \(f:\mathbb {I}\rightarrow \mathbb {I}\) is almost continuous (in the sense of Stallings) if every open set \(U\subset \mathbb {I}^2\) containing \(\Gamma (f)\) (i.e. a \(\Gamma \)-neighbourhood of f) contains the graph of some continuous function \(g:\mathbb {I}\rightarrow \mathbb {I}\).

Theorem 2.2

Let \(f:\mathbb {I}\rightarrow \mathbb {I}\). The following conditions are equivalent:

1. (i)

   f is an almost continuous function.

2. (ii)

   Every open set \(U \subset \mathbb {I}^2\) containing \(\Gamma (f)\) contains the graph of some continuous function having a peculiar point of the first kind.

3. (iii)

   Every open set \(U \subset \mathbb {I}^2\) containing \(\Gamma (f)\) contains the graph of some continuous function having a peculiar point of the second kind.

Proof

The implication 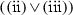\(\Rightarrow \) (i) is evident, so we will prove only implications (i)\(\Rightarrow \) (ii) and (i)\(\Rightarrow \) (iii).

Assume that f is almost continuous and 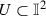is an open set containing \(\Gamma (f)\). Then there exists a continuous function \(\phi :\mathbb {I}\rightarrow \mathbb {I}\) such that \(\Gamma (\phi )\subset U\). Clearly, this function has a fixed point \(x_0\). Without loss of generality we may assume that 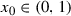. Let \(\varepsilon >0 \) be a number such that the square 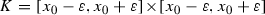is a subset of U. Fix a smaller square \(K_0\) with center at \(x_0\) and the edges parallel to the coordinate axes such that .

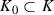Firstly we will prove that (i)\(\Rightarrow \) (ii). On the interval \(\mathrm{proj}_X(K_0)\) we may consider the classical construction of a Cantor-type set C of positive measure. Clearly, the ends of \(\mathrm{proj}_X(K_0)\) belong to C. Moreover, in the \(k^\mathrm{th}\) stage of construction we remove \(2^{k-1}\) open middle intervals denoted by 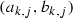, \(j=1,2,\ldots , 2^{k-1}\), respectively.

We will define a continuous function \(\tau :\mathbb {I}\rightarrow \mathbb {I}\) which fulfils conditions from (ii). For any \(n\in \mathbb {N}\) and 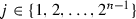let us consider the interval 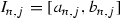. Let 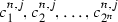be the points from 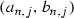which divide the interval \(I_{n,j}\) into \(2^n+1\) closed intervals of equal length. Put

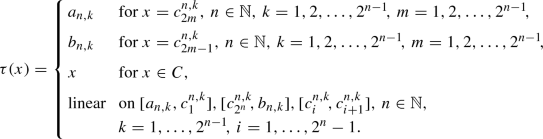
In this way we have defined \(\tau \) on the interval \(\mathrm{proj}_X(K_0)\). We put \(\tau (x)=\phi (x)\) on 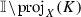and linear on 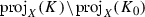so that \(\tau \) is continuous on the interval \(\mathbb {I}\). It is easy to see that \(\Gamma (\tau )\subset U\). We will show that this function has desired properties.

Let \(\Phi (C)\) be the set of all density points of the set C. By the Lebesgue Density Theorem (see [7]) we infer that \(\Phi (C)\cap C\ne \varnothing \). Let 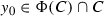and obviously, it is not the end of any interval from the complement of C (because if so, then \(y_0\) is not a density point of C). The point \(y_0\) belongs to C, hence from the definition of the function \(\tau \) we obtain 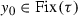. We shall show that \(y_0\) is a peculiar point of the first kind, so it fulfils conditions (A1), (B1) and (C1).

To see (A1), observe that for any \(\sigma >0\) one can find a neighbourhood W of \(y_0\) such that \(W\subset (y_0-\sigma , y_0+\sigma )\) and the ends of W belong to C and they do not belong to the closure of any component of the complement of C. Then \(\tau ^n(W)=W\) for any \(n\in \mathbb {N}\). Therefore, \(y_0\) is a stable point of \(\tau \) and, in consequence, it is an almost stable point of \(\tau \).

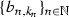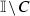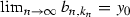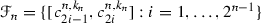Obviously, there is a strictly increasing sequence of the ends of intervals from such that . Put and 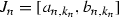. It is easy to see that 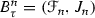is a \(\tau \)-bundle with dominating fibre. Since 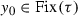one may easily show that \( B_{\tau }^n \xrightarrow [\scriptscriptstyle n\rightarrow \infty \,]{}y_0\). Moreover, \(h(B_{\tau }^n)\geqslant \log 2^{n-1}\). In consequence we obtain that 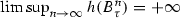so \(e_\tau (y_0)=+\infty \). Finally, \(y_0\) is an odd point of \(\tau \).

To show (B1) we prove first that \(\tau \) is 0-approximately continuous at \(y_0\). Evidently, \(y_0\) is a density point of C and 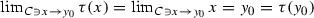. Moreover, since \(\tau \) is the identity function on C, it is easy to see that \(h(\tau , C)=0\). Indeed, take \(\varepsilon >0\). For any \(n\in \mathbb {N}\), if M is a \((\tau , C, \varepsilon , n)\)-separated set, then 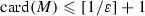(where 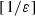means the integer part of \({1}/{\varepsilon }\)). To see that we observe first that for \(x \in M\subset C\subset \mathbb {I}\) and any we have \( \tau ^i(x)=x\). Then, if 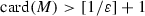, we could find two different points \(x, y\in M\) such that \(|x-y|<\varepsilon \). Hence \(|\tau ^i(x)-\tau ^i(y)|=|x-y|<\varepsilon \) for any \(i\in \{0, 1, \dots , n-1\}\), which is impossible. Finally, 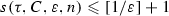. Therefore, 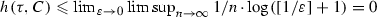, and consequently \(h(\tau , C)=0\), which means that \(\tau \) is 0-approximately continuous at \(y_0\).

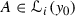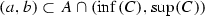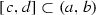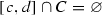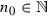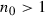The function \(\tau \) is not strongly 0-approximately continuous at \(y_0\). Assume contrary, that \(\tau \) is strongly 0-approximately continuous at \(y_0\). Then there exists an interval set for which \(h(\tau , A)=0\). Let be a non-empty interval. Since C is nowhere dense, then there is a non-empty interval such that . Clearly, one can find and such that and 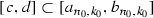. Analogously, as it was presented for the tent map one may show that there is 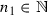for which 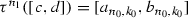. Observe, that by putting 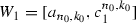and 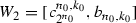we obtain 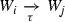for \(i,j\in \{1, 2\}\) and \(W_1\cap W_2=\varnothing \). From Lemma 1.1, we have 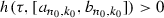. In consequence, Lemma 1.2 implicates that 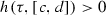, which is a contradiction with 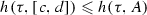. Finally, \(\tau \) is not strongly 0-approximately continuous at \(y_0\).

Now we shall show condition (C1) so we shall prove that \(\tau \) attracts positive entropy at \(y_0\). Clearly \(\tau \in \mathfrak {D}\).

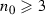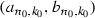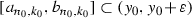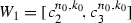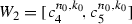Let \(\varepsilon >0\). Obviously, one can find and such that is a component of the complement of C such that . Put \(\delta =c_1^{n_0, k_0}\!-a_{n_0, k_0}\) and consider and . Obviously, \(W_1, W_2\) are disjoint closed sets and .

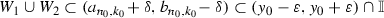Let \(g\in B(\tau , \delta )\cap \mathfrak {D}\). From the definition of \(\tau \) it follows that \(\tau (c_3^{n_0, k_0})=\tau (c_5^{n_0, k_0})=b_{n_0, k_0}\) and \(\tau (c_2^{n_0, k_0})=\tau (c_4^{n_0, k_0})=a_{n_0, k_0}\). Then 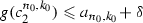, \(g(c_4^{n_0, k_0})\leqslant a_{n_0, k_0}+\delta \), 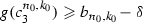and 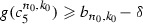. From the Darboux property it follows that 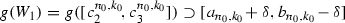and 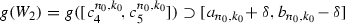. Thus 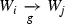for \(i,j\in \{1,2\}\). Lemma 1.1 implies that \(h(g, (y_0-\varepsilon , y_0+\varepsilon )\cap \mathbb {I})>0\) and \(\tau \) attracts positive entropy at \(y_0\). This finishes the proof of implication (i)\(\Rightarrow \) (ii).

Now we will prove the implication (i)\(\Rightarrow \) (iii). Denote the interval \(\mathrm{proj}_X(K_0)\) by 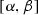and fix \(x_0\in (\alpha , \beta )\). Let 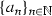, , 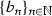, 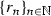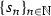be sequences such that

$$\begin{aligned} x_0< b_{n+1}<r_n<s_n<a_n<b_n<\beta \end{aligned}$$

for any \(n\in \mathbb {N}\) and the right-hand density of the set 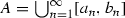at \(x_0\) be equal to 1.

Firstly, for any \(n\in \mathbb {N}\) we will define a function \(\tau _n\) on each 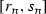by using the same method as in the previous part of the proof. Fix \(n\in \mathbb {N}\). Let \(a_1^n, a_2^n, \ldots , a_{2^n}^n\) be the points from 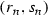which divide this interval into \(2^n+1\) closed intervals of equal length. Put

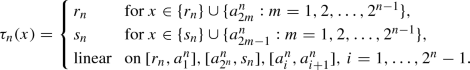
Define \(\tau \) on the set 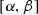by the formula

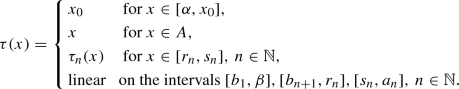
Moreover, we put \(\tau (x)=\phi (x)\) on 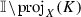and linear on 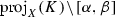so that \(\tau \) is continuous on the interval \(\mathbb {I}\). Obviously, \(\Gamma (\tau )\subset U\).

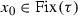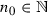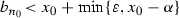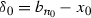We shall show that \(\tau \) fulfils all conditions from (iii). Observe that \(x_0\) is an odd point of \(\tau \). Indeed, obviously . Let \(\varepsilon >0\). There is such that . Put and 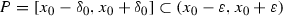. It is easy to see that \(\tau ^n(P)\subset P\) for any \(n\in \mathbb {N}\), which gives that \(x_0\) is an almost stable point of \(\tau \).

Moreover, by putting 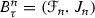, 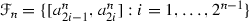and 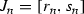, we can show, analogously to in the first part of the proof, that the entropy of \(\tau \) at \(x_0\) is infinite, which completes the proof of (A1).

To show condition (B1\('\)), consider sequences 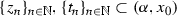convergent to \(x_0\) such that \(z_n<t_n<z_{n+1}\) for \(n\in \mathbb {N}\) and the left-hand density of 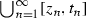at \(x_0\) is equal to 1. Obviously, for 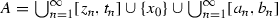we obtain that 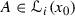and \(x_0\) is a density point of A. Moreover, we see at once that \(\lim _{A\ni x\rightarrow x_0} \tau (x)=\tau (x_0)\). Since \(\tau \) is constant on 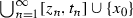and \(\tau (x)=x\) for 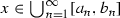we have that \(h(\tau ,A)=0\).

Similarly, like in the previous case we can prove that \(\tau \) satisfies condition (C1) (for any \(\varepsilon >0\) we will use some interval 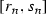contained in \((x_0-\varepsilon , x_0+\varepsilon )\) and divided into \(2^n+1\) parts each of length \(\delta \)). The proof of implication (i)\(\Rightarrow \) (iii) is thus complete. \(\square \)

robertsoune1982.blogspot.com

Source: https://link.springer.com/article/10.1007/s40879-018-0264-7

Share this post